发表于 | 更新于 | 分类于

第 1 章 算法概述

算法 (algorithm) 是一系列程序指令，用于处理特定的运算和逻辑问题。衡量算法优劣的主要标准是时间复杂度和空间复杂度。

数据结构 (data structure) 是数据的组织、管理和存储格式，其使用目的是为了高效地访问和修改数据。数据结构都有哪些组成方式呢?

  1. 线性结构：最简单的数据结构，包括数组、链表，以及由它们衍生出来的栈、队列、哈希表。
  2. 树：相对复杂的数据结构，其中比较有代表性的是二叉树，由它又衍生出了二叉堆之类的数据结构。
  3. 图：更为复杂的数据结构，因为在图中会呈现出多对多的关联关系。
  4. 其他数据结构：由基本数据结构变形而来，用于解决某些特定问题，如跳表、哈希链表、位图等。

时间复杂度 是对一个算法运行时间长短的量度，用大 O 表示，记作 T(n) = O(f(n))。

空间复杂度 是对一个算法在运行过程中临时占用存储空间大小的量度，用大 O 表示，记作 S(n) = O(f(n))。

第 2 章 数据结构基础

1. 数组

数组 (array) 是由有限个相同类型的变量所组成的有序集合。数组是最为简单、最为常用的数据结构。数组的物理存储方式是顺序存储，访问方式是随机访问。

数组的优势：利用下标就可以用常量时间 O(1) 找到对应元素。有一种高效查找元素的算法叫作二分查找，就是利用了数组的这个优势。

数组的劣势：由于数组元素连续紧密地存储在内存中，插入、删除元素都会导致大量元素被迫移动，其时间复杂度是 O(n)。

2. 链表

链表 (linked list) 是一种链式数据结构，由若干节点组成，每个节点包含指向下一节点的指针。链表的物理存储方式是随机存储，访问方式是顺序访问。查找链表节点的时间复杂度是 O(n)，插入、删除节点的时间复杂度是 O(1)。

3. 栈

栈 (stack) 是一种线性数据结构，可以用数组实现，也可以用链表实现。栈包含 入栈 (push) 和 出栈 (pop) 操作，遵循 先入后出 (FILO) 的原则，最早进入的元素存放的位置叫作 栈底 (bottom)，最后进入的元素存放的位置叫作 栈顶 (top)。

栈的应用：栈的输出顺序和输入顺序相反，所以栈通常用于对「历史」的回溯。例如实现递归的逻辑，就可以用栈来代替，因为栈可以回溯方法的调用链。栈还有一个著名的应用场景是面包屑导航，使用户在浏览页面时可以轻松地回溯到上一级或更上一级页面。

4. 队列

队列 (queue) 也是一种线性数据结构，可以用数组实现，也可以用链表实现。队列包含 入队 (enqueue) 和 出队 (dequeue) 操作，遵循 先入先出 (FIFO) 的原则。队列的出口端叫作 队头 (front)，队列的入口端叫作 队尾 (rear)。

队列的应用：队列的输出顺序和输入顺序相同，所以队列通常用于对「历史」的回放，也就是按照「历史」顺序，把「历史」重演一遍。例如在多线程中，争夺公平锁的等待队列，就是按照访问顺序来决定线程在队列中的次序的。再如网络爬虫实现网站抓取时，也是把待抓取的网站URL存入队列中，再按照存入队列的顺序来依次抓取和解析的。

物理结构：包括顺序存储结构（数组）和链式存储结构（链表）
逻辑结构：包括线性结构（顺序表、栈、队列）和非线性结构（树、图）

5. 散列表

散列表 也叫 哈希表 (hash table)，是存储 Key-Value 映射的集合。对于某一个 Key，散列表可以在接近 O(1) 的时间内进行读写操作。散列表本质上是一个数组，通过哈希函数实现 Key 和数组下标的转换，通过开放寻址法和链表法来解决哈希冲突。

开放寻址法：当一个 Key 通过哈希函数获得对应的数组下标已被占用时，我们可以「另谋高就」，寻找下一个空档位置。

链表法：Java 的集合类 HashMap 使用的就是链表法。HashMap 数组的每一个元素不仅是一个 Entry 对象，还是一个链表的头节点。每一个 Entry 对象通过 next 指针指向它的下一个 Entry 节点。当新来的 Entry 映射到与之冲突的数组位置时，只需要插入到对应的链表中即可。

第 3 章 树

1. 二叉树

二叉树 (binary tree) 是树的一种特殊形式，每一个节点最多有 2 个孩子节点。二叉树包含完全二叉树和满二叉树两种特殊形式：

  1. 满二叉树：所有非叶子节点都存在左右孩子，并且所有叶子节点都在同一层级上。

满二叉树

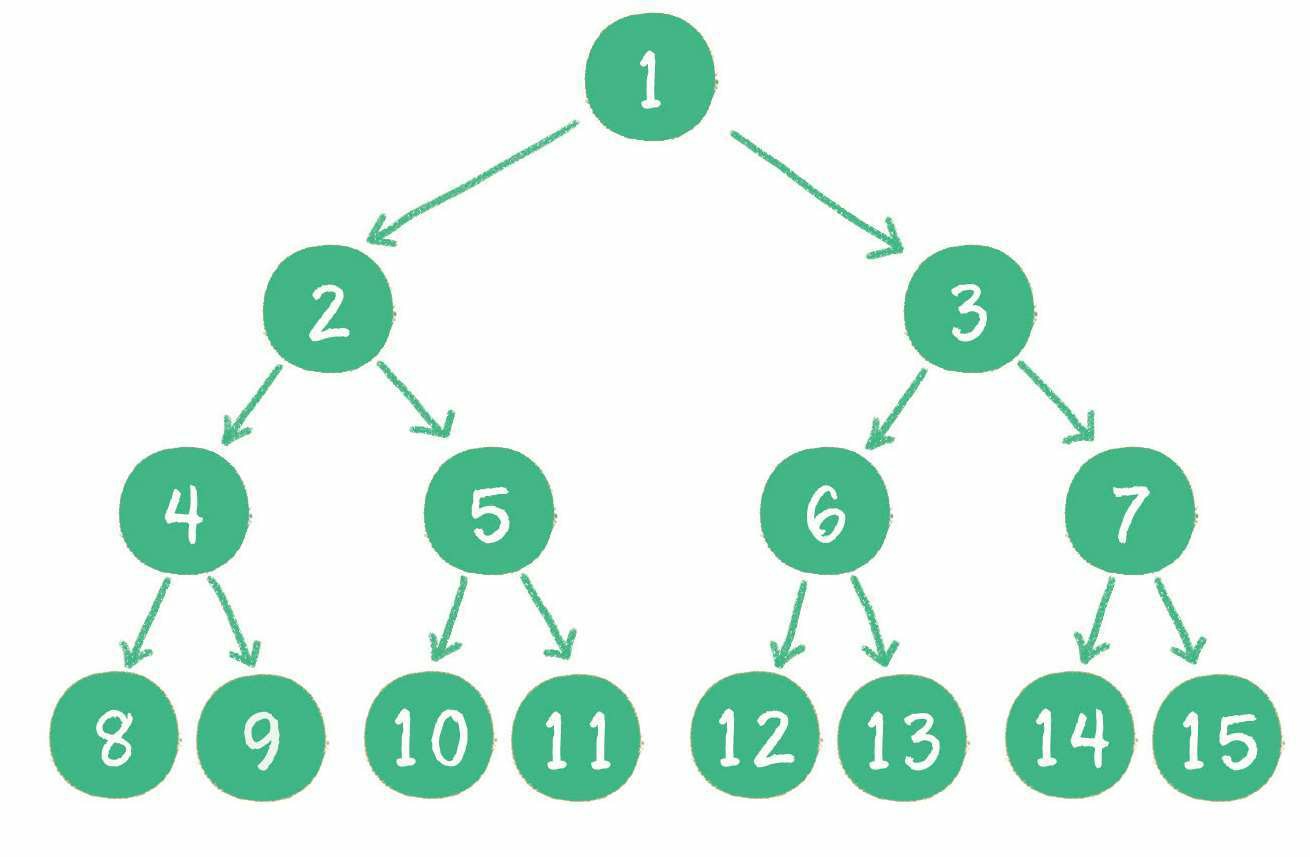
  1. 完全二叉树：如果一个树所有 n 个节点和同样深度的满二叉树的 1 到 n 的节点位置相同，则这个二叉树为完全二叉树。

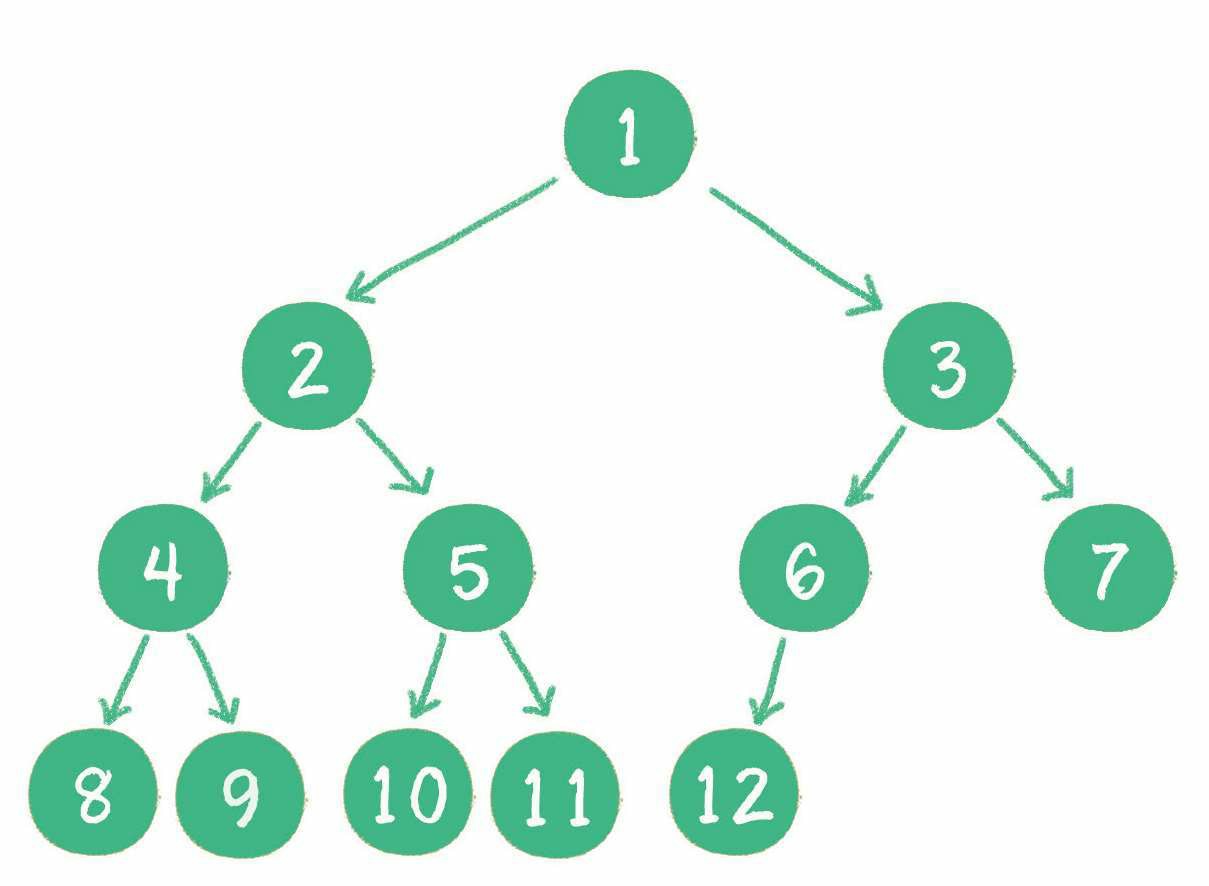
完全二叉树

完全二叉树的条件没有满二叉树那么苛刻：满二叉树要求所有分支都是满的；而完全二叉树只需保证最后一个节点之前的节点都齐全即可。

二叉树的应用

1. 查找

二叉查找树 (binary search tree) 在二叉树的基础上增加了二个条件：左子树上所有节点的值均小于根节点的值；右子树上所有节点的值均大于根节点的值。

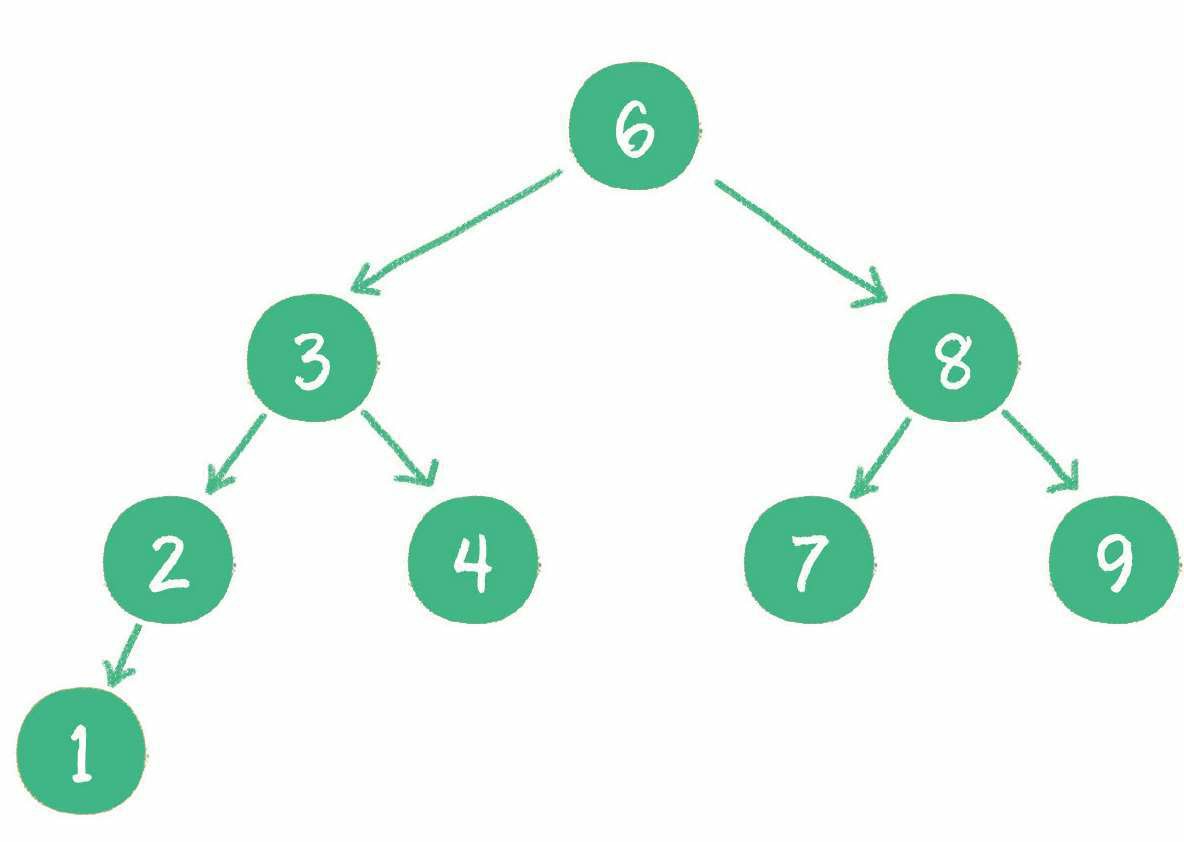
二叉查找树

例如上图中查找值为 4 的节点，步骤如下：

  1. 访问根节点 6，发现 4 < 6。
  2. 访问节点 6 的左孩子节点 3，发现 4 > 3。
  3. 访问节点 3 的右孩子节点 4，发现 4 = 4，这正是要查找的节点。

对于一个节点分布相对均衡的二叉查找树来说，如果节点总数是 n，那么搜索节点的时间复杂度就是 O(logn)，和树的深度是一样的。这种依靠比较大小来逐步查找的方式，和二分查找算法非常相似。

2. 排序

二叉排序树 (binary sort tree) 是二叉查找树的另一个名字，新插入的节点，同样要遵循二叉排序树的原则。例如插入新元素 5，由于 5 < 6，5 > 3，5 > 4，所以 5 最终会插入到节点 4 的右孩子位置。

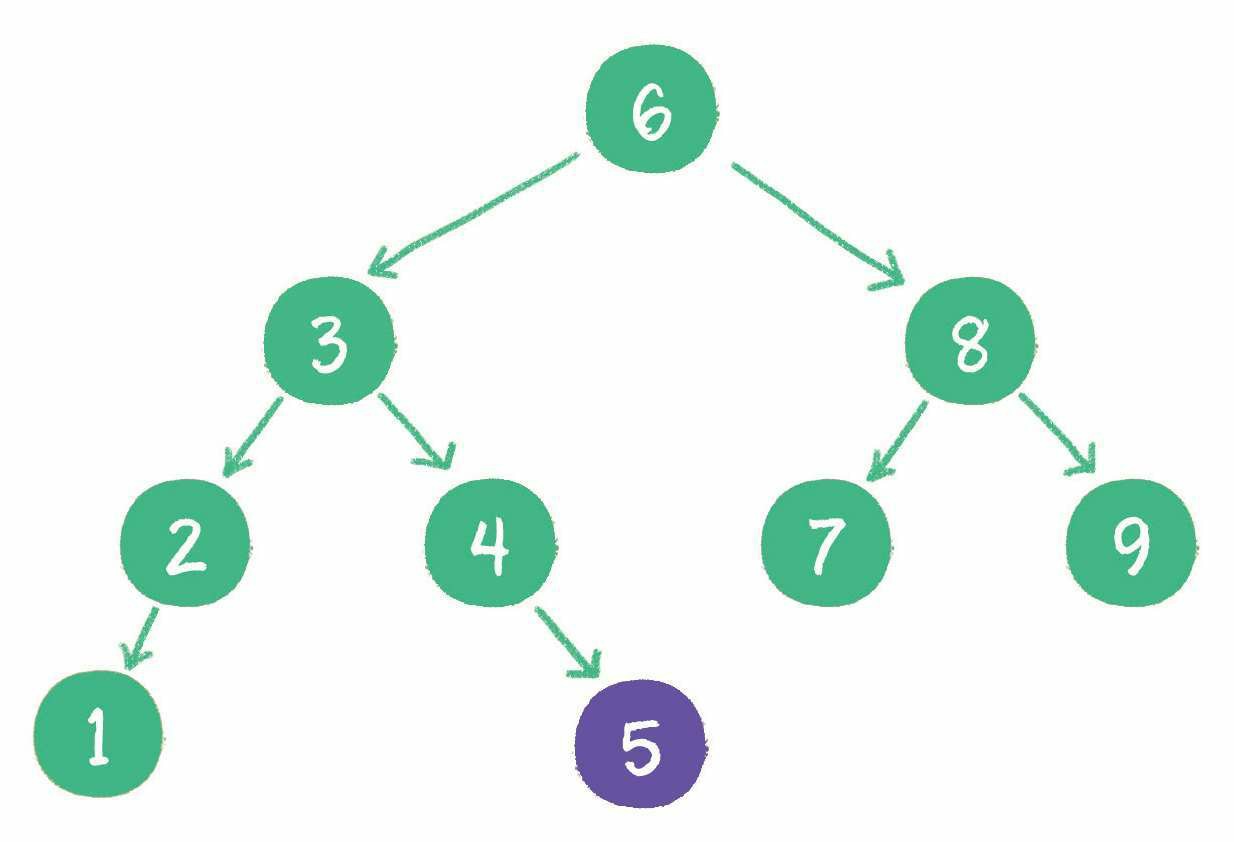
二叉排序树

这一切看起来很顺利，然而却隐藏着一个致命的问题。下面请试着在二叉查找树中依次插入 9、8、7、6、5、4，看看会出现什么结果。

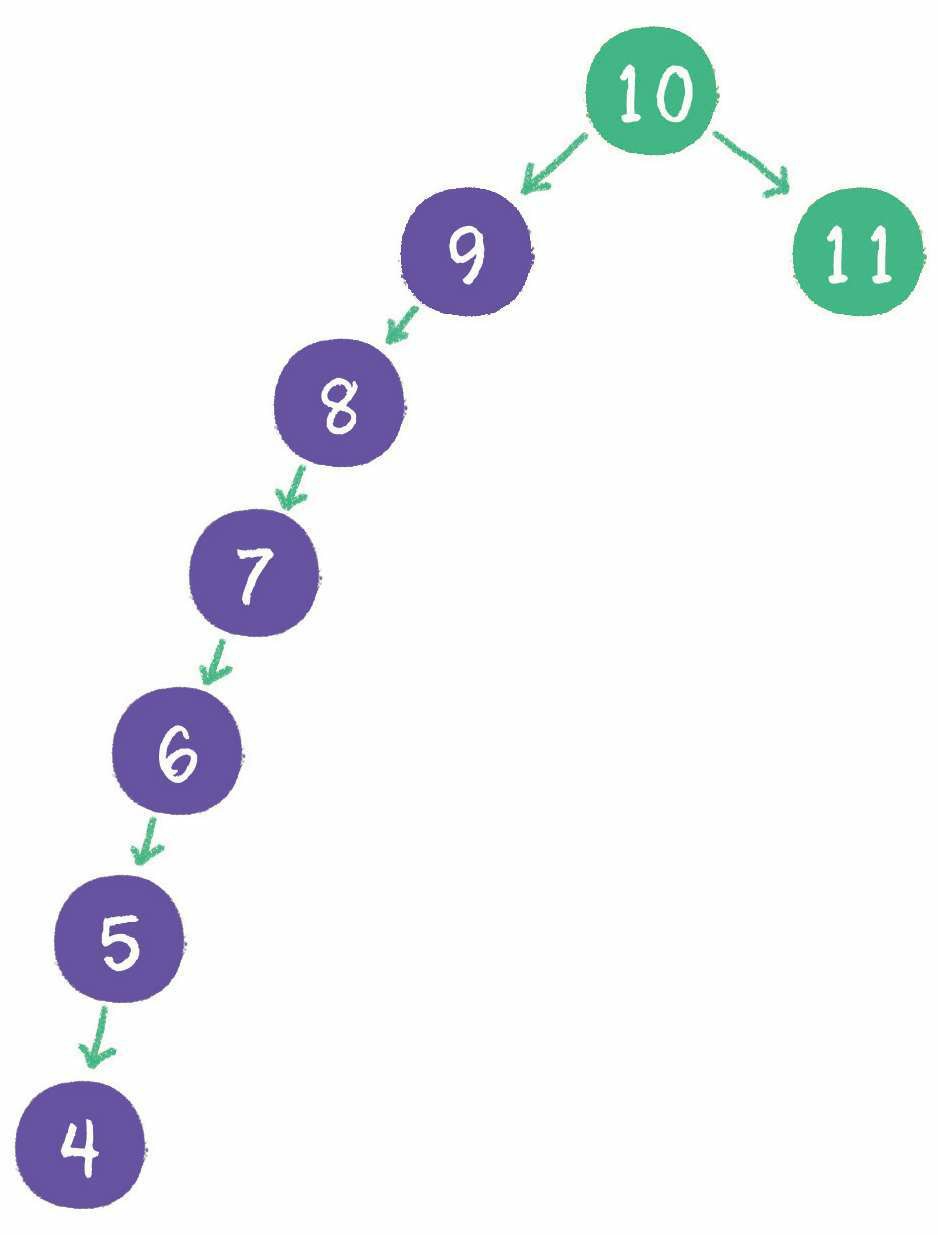
二叉排序树

不只是外观看起来变得怪异了，查询节点的时间复杂度也退化成了 O(n)。怎么解决这个问题呢？这就涉及二叉树的自平衡了。二叉树自平衡的方式有多种，如红黑树、AVL 树、树堆等。由于篇幅有限，本书就不 一一详细讲解了，感兴趣的读者可以查一查相关资料。

二叉树的遍历方式

遍历方式 输出顺序 宏观角度区分
前序遍历 根节点、左子树、右子树 深度优先遍历
中序遍历 左子树、根节点、右子树 深度优先遍历
后序遍历 左子树、右子树、根节点 深度优先遍历
层序遍历 广度优先遍历

深度优先遍历

绝大多数可以用递归解决的问题，其实都可以用另一种数据结构来解决，这种数据结构就是栈。因为递归和栈都有回溯的特性。

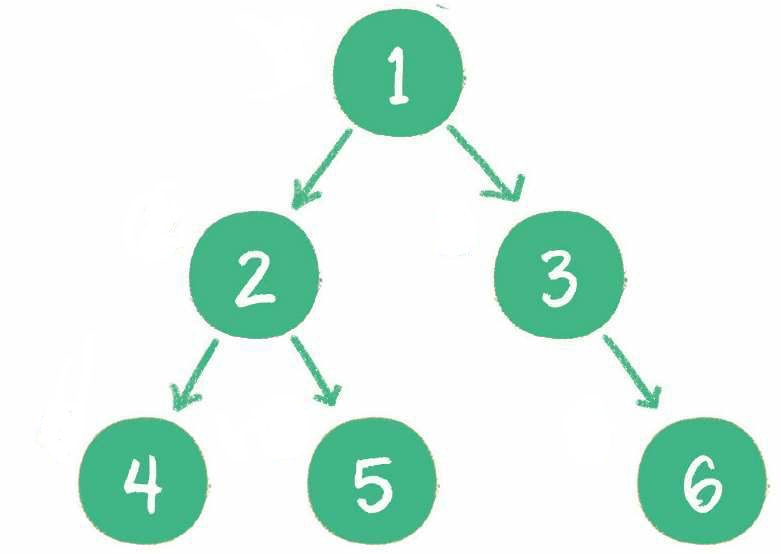
深度优先遍历

  1. 首先遍历二叉树的根节点 1，放入栈中。
  2. 遍历根节点 1 的左孩子节点 2，放入栈中。
  3. 遍历节点 2 的左孩子节点 4，放入栈中。
  4. 节点 4 既没有左孩子，也没有右孩子，我们需要回溯到上一个节点 2。栈已经存储了刚才遍历的路径。让旧的栈顶元素 4 出栈，就可以重新访问节点 2，得到节点 2 的右孩子节点 5。此时节点 2 已经没有利用价值，节点 2 出栈，节点 5 入栈。
  5. 节点 5 既没有左孩子，也没有右孩子，我们需要再次回溯，一直回溯到节点 1。所以让节点 5 出栈。根节点 1 的右孩子是节点 3，节点 1 出栈，节点 3 入栈。
  6. 节点 3 的右孩子是节点 6，节点 3 出栈，节点 6 入栈。
  7. 节点 6 既没有左孩子，也没有右孩子，所以节点 6 出栈。此时栈为空，遍历结束。

广度优先遍历

二叉树同一层次的节点之间是没有直接关联的，如何实现这种层序遍历呢？这里同样需要借助一个数据结构来辅助工作，这个数据结构就是队列。

![广度优先遍历](/Users/mayan/Desktop/《漫画算法 - 小灰的算法之旅》读书笔记/006.jpg)

  1. 根节点 1 进入队列。
  2. 节点 1 出队，输出节点 1，并得到节点 1 的左孩子节点 2、右孩子节点 3。让节点 2 和节点 3 入队。
  3. 节点 2 出队，输出节点 2，并得到节点 2 的左孩子节点 4、右孩子节点 5。让节点 4 和节点 5 入队。
  4. 节点 3 出队，输出节点 3，并得到节点 3 的右孩子节点 6。让节点 6 入队。
  5. 节点 4 出队，输出节点 4，由于节点 4 没有孩子节点，所以没有新 节点入队。
  6. 节点 5 出队，输出节点 5，由于节点 5 同样没有孩子节点，所以没 有新节点入队。
  7. 节点 6 出队，输出节点 6，节点 6 没有孩子节点，没有新节点入 队。

二叉堆

二叉堆是一种特殊的完全二叉树，分为最大堆和最小堆。在最大堆中，任何一个父节点的值，都大于或等于它左、右孩子节点的值；在最小堆中，任何一个父节点的值，都小于或等于它左、右孩子节点的值。

二叉堆的根节点叫作堆顶。最大堆和最小堆的特点决定了：最大堆的堆顶是整个堆中的最大元素；最小堆的堆顶是整个堆中的最小元素。

优先队列

优先队列分为最大优先队列和最小优先队列。

在最大优先队列中，无论入队顺序如何，当前最大的元素都会优先出队，这是基于最大堆实现的。

在最小优先队列中，无论入队顺序如何，当前最小的元素都会优先出队，这是基于最小堆实现的。

发表于 | 更新于 | 分类于

第 1 章 面试的流程

1. 简历中描述项目的 STAR 模型

a. Situation 简短的项目背景。比如项目的规模，开发的软件的功能、目标用户等。

b. Task 自己完成的任务。在用词上要区分「参与」和「负责」，面试官看到简历上应聘者「负责」了某个项目，他可能就会问项目的总体框架设计、核心算法、团队合作等问题。

c. Action 为完成任务做了哪些工作，是怎么做的。做系统设计的，可以介绍系统架构的特点；做软件开发的，可以写基于什么工具在哪个平台下应用了哪些技术。

d. Result 自己的贡献。这方面的信息最好能用数字加以说明，如果参与功能开发，可以说按时完成了多少功能；如果做优化，可以说性能提高的百分比是多少；如果是维护，可以说修改了多少个 Bug。

举个例子：Winforms 是微软 .NET 中的一个成熟的 UI 平台（ Situation ）。本人的工作是在添加少量新功能之外主要负责维护已有的功能（ Task ）。新的功能主要是让 Winforms 的控件风格和 Vista、Windows 7 的风格保持一致。在维护方面，对于较难的问题，我用 WinDbg 等工具进行调试（ Action ）。在过去两年中，我共修改了超过 200 个 Bug（ Result ）。

除此之外，面试官针对项目经验最常问的问题包括如下几个类型：

a. 你在该项目中碰到最大的问题是什么，你是怎么解决的？
b. 从这个项目中你学到了什么？
c. 什么时候会和其他团队成员（包括开发人员、测试人员、设计人员、项目经理等）有什么样的冲突，你们是怎么解决冲突的？

2. 简历中技能的描述

除应聘者参与过的项目之外，面试官可能针对简历上提到的技能提出问题，和描述项目时要注意「参与」和「负责」一样，描述技能掌握程度时也要注意「了解」、「熟悉」和「精通」的区别。

了解 指对某项技术只是上过课或者看过书，但没有做过实际的项目。通常不建议在简历中列出只是肤浅地了解一点的技能，除非这项技术应聘的职位需要。

熟悉 指在项目中使用某项技术已经有较长的时间，通过查阅相关的文档可以独立解决大部分问题。简历中我们描述技能的掌握程度大部分应该是「熟悉」。

精通 指我们对一项技术使用的得心应手，在项目开发过程中，同事向我们请教这个领域的问题时，我们都有信心也有能力解决。

3. 回答「为什么跳槽」

笔者自己跳过几次槽，从 Autodesk 跳槽到微软，再从微软跳槽到思科，后来又从思科回到了微软。

在微软面试被问到为什么要跳槽时，笔者的回答是：我在 Autodesk 开发的软件 Civil 3D 是一款面向土木行业的设计软件。如果我想在现在的职位上得到提升，就必须加强土木行业的学习，可我对诸如计算土方量、道路设计等没有太多兴趣，因此出来寻找机会。

在微软工作两年半之后去思科面试的时候，笔者的回答是：我在微软的主要工作是开发和维护 .NET 的 UI 平台 Winforms。由于 Winforms 已经非常成熟，不需要添加多少新功能，因此我的大部分工作是维护和修改 Bug。两年下来，调试的能力得到了很大的提高，但长期如此，自己的软件开发和设计能力将不能得到提高，因此想出来寻找可以设计和开发系统的职位。同时，我在过去几年里的工作都是开发桌面软件，对网络了解甚少，因此希望下一个工作能与网络相关。众所周知，思科是一家网络公司，这里的软件和系统或多或少都离不开网络，因此我对思科的职位很感兴趣。

4. 技术面试环节

面试官在通过简历及行为面试大致了解应聘者的背景之后，接下来就要开始技术面试了。总体来说他们都会关注应聘者的 5 种素质：

a. 基础知识扎实全面，包括编程语言、数据结构、算法。其中数据结构是考察的重点，应聘者需要熟练掌握链表、树、栈、队列和哈希表等数据结构，以及它们的操作。对于算法，大部分公司都会注重考查查找和排序，其中重点需要掌握二分查找、归并排序和快速排序，因为很多面试题都只是这些算法的变体而已。

b. 能写出正确的、完整的、鲁棒的高质量代码。技术面试的面试官一般都是程序员，他们通常没有那么多想法，题目做对、做完整了，就让你通过面试。所以，面试官除了希望应聘者的代码能够完成基本的功能，还会关注应聘者是否考虑了边界条件、特殊输入及错误处理。

c. 能思路清晰地分析、解决复杂问题。有时候面试官会有意出一些比较复杂的问题，甚至不期待应聘者能在面试不到一个小时的时间里给出完整的答案，他更看重的是应聘者是否有清晰的思路。所以我们可以：画图使抽象问题形象化，举例使抽象问题具体化，分解使复杂问题简单化。

d. 能从时间、空间复杂度两方面优化算法效率。想要优化代码的效率，我们需要熟知各种数据结构的优缺点，并能选择合适的数据结构解决问题。

e. 具备优秀的沟通能力、学习能力、发散思维能力等。随着软件系统的规模越来越大，软件开发已经告别了单打独斗的年代，程序员与他人的沟通变得越来越重要。在面试过程中，面试官会观察应聘者在介绍项目经验或者算法思路时是否观点明确、逻辑清晰，并以此判断其沟通能力的强弱。另外，面试官也会从应聘者说话的神态和语气来判断他是否有团队合作的意识。对于学习能力，通常面试官有两种办法考查应聘者的学习能力。第一种方法是询问应聘者最近在看什么书、从中学到了哪些新技术。第二种方法是抛出一个新概念，接下来会观察应聘者能不能在较短的时间内理解并解决相关的问题。

5. 回答「你还有什么问题吗」

推荐问的问题是与应聘的职位或者项目相关的问题。

第 2 章 面试需要的基础知识

1. 数据结构 - 数组

数组可以说是最简单的一种数据结构，它占据一块连续的内存并按照顺序存储数据。创建数组时，我们首先指定数组的容量大小，然后根据大小分配内存。因此数组的空间效率不是很好，经常会有空闲的区域没有得到充分利用。

由于数组中的内存是连续的，于是可以根据下标在 O(1) 时间读 / 写任何元素，我们可以根据数组时间效率高的优点，用数组来实现简单的哈希表：把数组的下标设为哈希表的 key，数组中每一个数字设为哈希表的 value。

面试题 3 - 1

题目：找出数组中重复的数字。在一个长度为 n 的数组里的所有数字都在 0 ~ n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。例如，如果输入长度为 7 的数组 { 2, 3, 1, 0, 2, 5, 3 }，那么对应的输出是重复的数字 2 或者 3。

方法一，将数组排序，然后从头到尾扫描排序后的数组就可以了。排序一个长度为 n 的数组的时间复杂度为 O(nlogn)。

方法二，从头到尾扫描数组的每个数字，每扫描到一个数字的时候，都可以用 O(1) 的时间来判断哈希表里是否已经包含了该数字，如果哈希表里还没有这个数字，就把它加入哈希表；如果哈希表里已经存在该数字，就找到一个重复的数字。这个算法的时间复杂度是 O(n)，但它提高时间效率是以一个大小为 O(n) 的哈希表为代价的。

方法三，如果这个数组中没有重复的数字，那么当数组排序之后数字 i 将出现在下标为 i 位置。现在让我们重排这个数组，从头到尾扫描数组的每个数字，首先比较这个数字 m 是不是等于 i，如果是，接着扫描下一个数字；如果不是，再拿它和第 m 个数字进行比较，如果它和第 m 个数字相等，就找到了一个重复的数字（该数字在下标为 i 和 m 的位置都出现了），如果它和第 m 个数字不相等，就把第 i 个数字和第 m 个数字交换，把 m 放到属于它的位置。接下来再重复这个比较、交换的过程，直到我们发现一个重复的数字。这个算法的时间复杂度是 O(n)，控件复杂度为 O(1)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
int duplicate(int numbers[], int length) {
    
    if (numbers == NULL) {
        return -1;
    }
    
    for (int i = 0; i < length; ++i) {
        if (numbers[i] < 0 || numbers[i] > length - 1) {
            return -1;
        }
    }
    
    for (int i = 0; i < length; ++i) {
        while (numbers[i] != i) {
            if (numbers[i] == numbers[numbers[i]]) {
                return numbers[i];
            }
            // 交换 numbers[i] 和 numbers[numbers[i]]
            int temp = numbers[i];
            numbers[i] = numbers[temp];
            numbers[temp] = temp;
        }
    }
    
    return -1;
}

int main(int argc, const char * argv[]) {
    
    int numbers[] = { 2, 1, 3, 1, 4 };
    
    int duplication = duplicate(numbers, sizeof(numbers) / sizeof(int));

    if (duplication < 0) {
        printf("数组中没有重复的数字，或者输入无效\n");
    } else {
        printf("数组中有重复的数字，其中一个重复的数字为 %d\n", duplication);
    }
    
    return 0;
}

面试题 3 - 2

题目：不修改数组找出重复的数字。在一个长度为 n 的数组里的所有数字都在 1 ~ n-1 的范围内，所以数组中至少有一个数字是重复的。请找出数组中任意一个重复的数字，但不能修改输入的数组。例如，如果输入长度为 7 的数组 { 2, 3, 5, 4, 3, 2, 6 }，那么对应的输出是重复的数字 2 或者 3。

我们把从 1 ~ n-1 的数字从中间的数字 m 分为两部分，前面一半为 1 ~ m，后面一半为 m+1 ~ n-1。如果 1 ~ m 的数字的数目超过 m，那么这一半的区间里一定包含重复的数字；否则，另一半区间里一定包含重复的数字。我们继续把包含重复数字的区间一分为二，直到找到一个重复的数字。这个过程和二分查找算法类似，只是多了一步统计区间里数字的数目。这个算法的时间复杂度是 O(nlogn)，空间复杂度为 O(1)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
int getDuplication(const int* numbers, int length) {
    
    if (numbers == NULL) {
        return -1;
    }
    
    int start = 1;
    int end = length - 1;
    while (start <= end) {
        int middle = ((end - start) >> 1) + start;
        
        int count = 0;
        for (int i = 0; i < length; i++) {
            if (numbers[i] >= start && numbers[i] <= middle) {
                ++count;
            }
        }
        
        if (start == end) {
            if (count > 1) {
                return start;
            }
            break;
        }
        
        if (count > (middle - start + 1)) {
            end = middle;
        } else {
            start = middle + 1;
        }
    }
    
    return -1;
}

int main(int argc, const char * argv[]) {
    
    int numbers[] = { 2, 1, 3, 1, 4 };

    int duplication = getDuplication(numbers, sizeof(numbers) / sizeof(int));
    
    if (duplication < 0) {
        printf("数组中没有重复的数字，或者输入无效\n");
    } else {
        printf("数组中有重复的数字，其中一个重复的数字为 %d\n", duplication);
    }
    
    return 0;
}

面试题 4

题目：二维数组中的查找。在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。例如，从下面的矩阵中查找数字 7

1
2
3
4
1    2    8    9
2    4    9    12
4    7    10   13
6    8    11   15

首先选取数组中右上角的数字，如果该数字等于要查找的数字，则查找过程结束。如果该数字大于要查找的数字，则剔除这个数字所在的列。如果该数字小于要查找的数字，则剔除这个数字所在的行。这样每一步都可以缩小查找的范围，直到找到要查找的数字，或者查找范围为空。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int main(int argc, const char * argv[]) {
    
    int matrix[4][4] = { { 1, 2, 8, 9 }, { 2, 4, 9, 12 }, { 4, 7, 10, 13 }, { 6, 8, 11, 15 } };
    int number = 7;
    
    int maxRow = sizeof(matrix) / sizeof(matrix[0]) - 1;
    int maxCol = sizeof(matrix[0]) / sizeof(int) - 1;
    int row = 0;
    int col = maxCol;
    while (row <= maxRow && col >= 0) {
        if (matrix[row][col] == number) {
            break;
        } else if (matrix[row][col] > number) {
            --col;
        } else {
            ++row;
        }
    }
    
    if (row <= maxRow && col >= 0) {
        printf("已找到数字 %d，坐标为 [%d, %d]\n", number, row, col);
    } else {
        printf("没有找到数字 %d\n", number);
    }
    
    return 0;
}

2. 数据结构 - 字符串

字符串是由若干字符组成的序列，C/C++ 中每个字符串都以字符 \0 作为结尾，这样我们就能很方便地找到字符串的最后尾部。但由于这个特点，每个字符串中都有一个额外字符的开销，稍不留神就会造成字符串的越界。

1
2
3
4
5
char str[] = "012345";
printf("字符串长度为 %lu\n", sizeof(str));
if (str[6] == '\0') {
    printf("字符串最后一位为 '\\0'\n");
}

为了节省内存，C/C++ 把常量字符串放到单独的一个内存区域，当几个指针赋值给相同的常量字符串时，它们实际上会指向相同的内存地址。但用常量内存初始化数组，情况却有所不同。运行下面的代码，得到的结果是什么？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
char str1[] = "hello world";
char str2[] = "hello world";

char* str3 = "hello world";
char* str4 = "hello world";

if (str1 == str2) {
    printf("str1 和 str2 相同\n");
} else {
    printf("str1 和 str2 不相同\n");
}

if (str3 == str4) {
    printf("str3 和 str4 相同\n");
} else {
    printf("str3 和 str4 不相同\n");
}

str1 和 str2 是两个字符串数组，我们会为它们分配两个长度为 12 字节的空间，并把 hello world 的内容分别复制到数组中去。这是两个初始地址不同的数组，因此 str1 和 str2 的值也不相同。输出 str1 和 str2 不相同。

str3 和 str4 是两个指针，我们无须为它们分配内存以存储字符串的内容，而只需要把它们指向 hello world 在内存中的地址就可以了。由于 hello world 是常量字符串，它在内存中只有一个拷贝，因此 str3 和 str4 指向的是同一个地址。输出 str3 和 str4 相同。

面试题 5

题目：替换空格。请实现一个函数，把字符串中的每个空格替换成 %20。例如，输入 We are happy. 则输出 We%20are%20happy.。

在网络编程中，如果 URL 参数中含有特殊字符，则可能导致服务器无法获得正确的参数值，我们需要将这些特殊符号转换成服务器可以识别的字符。转换的规则是在 % 后面跟上 ASCII 码的两位十六进制的表示。

方法一，从头到尾扫描字符串，每次碰到空格字符的时候进行替换。由于是把 1 个字符替换成 3 个字符，我们必须要把空格后面所有的字符都后移 2 字节，否则就有两个字符被覆盖了。假设字符串的长度是 n，对每个空格字符，需要移动后面 O(n) 个字符，因此对于含有 O(n) 个空格字符的字符串而言，总的时间效率是 O(n²)。

方法二，首先遍历一次字符串，统计出字符串中空格的总数，计算替换后的字符串的总长度。以前面的字符串 We are happy 为例，这个字符串的长度是 14（包括结尾符号 \0），里面有两个空格，因此替换之后字符串的长度是 18。

我们从字符串的后面开始复制和替换。首先准备两个指针 P1 和 P2，P1 指向原始字符串的末尾，P2 指向替换后的字符串的末尾。接下来我们向前移动指针 P1，逐个把它指向的字符复制到 P2 指向的位置。碰到空格之后，把 P1 向前移动 1 格，在 P2 之前插入字符串 %20，同时也要把 P2 向前移动 3 格。从上面的分析中可以看出，所有的字符都只复制（移动）一次，因此这个算法的时间效率是 O(n)，比第一个方法要快。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
int main(int argc, const char * argv[]) {
    
    char str[100] = "We are happy.";
    
    int length = 0;  // 字符串的实际长度
    int newLength = 0;  // 把空格替换成 '%20' 之后的长度
    for (int i = 0; i < sizeof(str) / sizeof(char); i++) {
        
        length = length + 1;
        newLength = newLength + ((str[i] == ' ') ? 3 : 1);
        
        if (str[i] == '\0') {
            break;
        }
    }
   
    int index = length;
    int newIndex = newLength;
    while (index >= 0 && newIndex > index) {
        if (str[index] == ' ') {
            str[newIndex--] = '0';
            str[newIndex--] = '2';
            str[newIndex--] = '%';
        } else {
            str[newIndex--] = str[index];
        }
        --index;
    }
    
    printf("%s\n", str);
    
    return 0;
}

3. 数据结构 - 链表

我们说链表是一种动态数据结构，是因为在创建链表时，无须知道链表的长度。当插入一个节点时，我们只需要为新节点分配内存，然后调整指针的指向来确保新节点被链接到链表当中。内存分配不是在创建链表时一次性完成的，而是每添加一个节点分配一次内存。由于没有闲置的内存，链表的空间效率比数组高。

面试题 6

题目：从尾到头打印链表。输入一个链表的头节点，从尾到头反过来打印出每个节点的值。链表节点定义如下：

1
2
3
4
struct ListNode {
    int m_nKey;
    ListNode* m_pNext;
}

方法一，很多人第一反应是从头到尾输出将会比较简单，于是我们很自然地想到把链表中的链接节点的指针反转过来，改变链表的方向，然后就可以从头到尾输出了。但是是否允许在打印链表的时候修改链表的结构，这取决于面试官的要求，因此在面试的时候我们要询问清楚面试官的要求。

方法二，我们可以用栈实现「后进先出」这种顺序，每经过一个节点的时候，把该节点放到一个栈中。当遍历完整个链表后，再从栈顶开始逐个输出节点的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
typedef struct listNode {
    int m_nValue;
    struct listNode* m_pNext;
} ListNode;

// 创建一个链表元素
ListNode* CreateListNode(int value) {
    ListNode* pNode = malloc(sizeof(ListNode));  // 分配地址
    pNode->m_nValue = value;
    pNode->m_pNext = NULL;
    
    return pNode;
}

// 链接两个链表元素
void ConnectListNodes(ListNode* pCurrent, ListNode* pNext) {
    pCurrent->m_pNext = pNext;
}

int main(int argc, const char * argv[]) {
    
    ListNode* pNode1 = CreateListNode(1);
    ListNode* pNode2 = CreateListNode(2);
    ListNode* pNode3 = CreateListNode(3);
    ListNode* pNode4 = CreateListNode(4);
    ListNode* pNode5 = CreateListNode(5);
    
    ConnectListNodes(pNode1, pNode2);
    ConnectListNodes(pNode2, pNode3);
    ConnectListNodes(pNode3, pNode4);
    ConnectListNodes(pNode4, pNode5);
    
    ListNode* pNode = pNode1;
    
    int nodes[100] = {};
    int num = 0;
    while (pNode != NULL) {
        nodes[num] = pNode->m_nValue;
        pNode = pNode->m_pNext;
        num++;
    }
    
    for (int i = num - 1; i >= 0; i--) {
        printf("%d\t", nodes[i]);
    }
    printf("\n");
    
    return 0;
}

方法三，既然想到了用栈来实现这个函数，而递归在本质上就是一个栈结构。要实现反过来输出链表，我们每访问到一个节点的时候，先递归输出它后面的节点，再输出该节点自身，这样链表的输出结果就反过来了。虽然基于递归的代码看起来很简洁，但有一个问题：当链表非常长的时候，就会导致函数调用的层级很深，从而有可能导致函数调用栈溢出。显然用栈基于循环实现的代码的鲁棒性要好一些。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void PrintListReversingly_Recursively(ListNode* pHead) {
    if (pHead->m_pNext != NULL) {
        PrintListReversingly_Recursively(pHead->m_pNext);
    }
    printf("%d\t", pHead->m_nValue);
}

int main(int argc, const char * argv[]) {

    ListNode* pNode1 = CreateListNode(1);
    ListNode* pNode2 = CreateListNode(2);
    ListNode* pNode3 = CreateListNode(3);
    ListNode* pNode4 = CreateListNode(4);
    ListNode* pNode5 = CreateListNode(5);
    
    ConnectListNodes(pNode1, pNode2);
    ConnectListNodes(pNode2, pNode3);
    ConnectListNodes(pNode3, pNode4);
    ConnectListNodes(pNode4, pNode5);
    
    PrintListReversingly_Recursively(pNode1);
    
    return 0;
}

4. 数据结构 - 树

面试的时候提到的树，大部分是二叉树，其中最重要的操作莫过于遍历，通常树有如下几种遍历方式：

  • 前序遍历：先访问根节点，再访问左子节点，最后访问右子节点。图中前序遍历的顺序是 10、6、4、8、14、12、16；
  • 中序遍历：先访问左子节点，再访问根节点，最后访问右子节点。图中中序遍历的顺序是 4、6、8、10、12、14、16；
  • 后序遍历：先访问左子节点，再访问右子节点，最后访问根节点。图中后序遍历的顺序是 4、8、6、12、16、14、10；
  • 宽度优先遍历：先访问树的第一层节点，再访问树的第二层节点，直到访问到最下面一层节点。图中宽度优先遍历的顺序是 10、6、14、4、8、12、16。

IMG001

二叉树有很多特例，二叉搜索树就是其中之一。在二叉搜索树中，左子节点总是小于或等于根节点，右子节点总是大于或等于根节点，上图中的二叉树就是一颗二叉搜索树。我们可以平均在 O(logn) 的时间内根据数值在二叉搜索树中找到一个节点。

二叉树的另外两个特例是堆和红黑树。堆分为最大堆和最小堆，在最大堆中根节点的值最大，在最小堆中根节点的值最小，有很多需要快速找到最大值或者最小值的问题都可以用堆来解决。红黑树是把树中的节点定义为红、黑两种颜色，并通过规则确保从根节点到叶节点的最长路径的长度不超过最短路径的二倍。在 C++ 的 STL 中，set、multiset、map、multimap 等数据结构都是基于红黑树实现的。

面试题 7

题目：重建二叉树。输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如，输入前序遍历序列 { 1, 2, 4, 7, 3, 5, 6, 8 } 和中序遍历序列 { 4, 7, 2, 1, 5, 3, 8, 6 }，则重建如下图所示的二叉树并输出它的头节点。二叉树节点的定义如下：

1
2
3
4
5
typedef struct binaryTreeNode {
    int m_nValue;
    struct binaryTreeNode* m_pLeft;
    struct binaryTreeNode* m_pRight;
} BinaryTreeNode;

前序遍历序列的第一个数字 1 就是根节点的值，根据中序遍历的特点，在根节点的值 1 前面的 3 个数字都是左子树节点的值，位于 1 后面的 4 个数字都是右子树节点的值。然后我们可以用同样的方法分别构建左、右子树。也就是说，接下来的事情可以用递归的方法去完成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
typedef struct binaryTreeNode {
    int m_nValue;
    struct binaryTreeNode* m_pLeft;
    struct binaryTreeNode* m_pRight;
} BinaryTreeNode;

// 创建一个节点元素
BinaryTreeNode* CreateBinaryTreeNode(int value) {
    BinaryTreeNode* pNode = malloc(sizeof(BinaryTreeNode));  // 分配地址
    pNode->m_nValue = value;
    pNode->m_pLeft = NULL;
    pNode->m_pRight = NULL;
    
    return pNode;
}

// 链接父子节点元素
void ConnectTreeNodes(BinaryTreeNode* pParent, BinaryTreeNode* pLeft, BinaryTreeNode* pRight) {
    pParent->m_pLeft = pLeft;
    pParent->m_pRight = pRight;
}

void PrintTree(const BinaryTreeNode* pRoot) {
    if (pRoot == NULL) {
        printf("没有根节点\n");
        return;
    }
    printf("根节点 [%d]\t", pRoot->m_nValue);
    pRoot->m_pLeft == NULL ? printf("左子节点 [无]\t") : printf("左子节点 [%d]\t", pRoot->m_pLeft->m_nValue);
    pRoot->m_pRight == NULL ? printf("右子节点 [无]") : printf("右子节点 [%d]", pRoot->m_pRight->m_nValue);
    printf("\n");
    
    if (pRoot->m_pLeft != NULL) {
        PrintTree(pRoot->m_pLeft);
    }
    if (pRoot->m_pRight != NULL) {
        PrintTree(pRoot->m_pRight);
    }
}

BinaryTreeNode* ConstructCore(int* startPreorder, int* endPreorder, int* startInorder, int* endInorder) {
    // 前序遍历序列的第一个数字是根结点的值
    int rootValue = startPreorder[0];
    BinaryTreeNode* root = CreateBinaryTreeNode(rootValue);
    
    if (startPreorder == endPreorder) {
        if (startInorder == endInorder && *startPreorder == *startInorder) {
            return root;
        }
        return NULL;
    }
    
    // 在中序遍历中找到根结点的值
    int* rootInorder = startInorder;
    while (rootInorder <= endInorder && *rootInorder != rootValue) {
        ++rootInorder;
    }
    
    if (rootInorder == endInorder && *rootInorder != rootValue) {
        return NULL;
    }
    
    long leftLength = rootInorder - startInorder;
    if (leftLength > 0) {
        // 构建左子树
        root->m_pLeft = ConstructCore(startPreorder + 1, startPreorder + leftLength, startInorder, rootInorder - 1);
    }
    if (leftLength < endPreorder - startPreorder) {
        // 构建右子树
        root->m_pRight = ConstructCore(startPreorder + leftLength + 1, endPreorder, rootInorder + 1, endInorder);
    }
    return root;
}

BinaryTreeNode* Construct(int *preorder, int* inorder, int length) {
    if (preorder == NULL || inorder == NULL || length <= 0) {
        return NULL;
    }
    return ConstructCore(preorder, preorder + length - 1, inorder, inorder + length - 1);
}

int main(int argc, const char * argv[]) {
    
    int preorder[8] = { 1, 2, 4, 7, 3, 5, 6, 8 };
    int inorder[8] = { 4, 7, 2, 1, 5, 3, 8, 6 };
    
    BinaryTreeNode* root = Construct(preorder, inorder, 8);  // 生成树
    PrintTree(root);  // 打印树
    
    return 0;
}

面试题 8

题目：二叉树的下一个节点。给定一棵二叉树和其中的一个节点，如何找出中序遍历序列的下一个节点？树中的节点除了有两个分别指向左、右子节点的指针，还有一个指向父节点的指针。

如下图的二叉树的中序遍历序列是 { d, b, h, e, i, a, f, c, g }，我们将以这棵树为例来分析如何找出二叉树的下一个节点。

IMG002

  • 如果这个节点有右子树，那么它下一个节点就是它的右子树中的最左子节点；
  • 如果这个节点没有右子树，但是这个节点是它父节点的左子节点，那么它的下一个节点就是它的父节点；
  • 如果这个节点没有右子树，并且这个节点是它父节点的右子节点，我们可以沿着指向父节点的指针一直向上遍历，直到找到一个是它父节点的左子节点的节点，那么这个节点的父节点就是我们要找的下一个节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
typedef struct binaryTreeNode {
    char m_nValue;
    struct binaryTreeNode* m_pLeft;
    struct binaryTreeNode* m_pRight;
    struct binaryTreeNode* m_pParent;
} BinaryTreeNode;

// 创建一个节点元素
BinaryTreeNode* CreateBinaryTreeNode(char value) {
    BinaryTreeNode* pNode = malloc(sizeof(BinaryTreeNode));  // 分配地址
    pNode->m_nValue = value;
    pNode->m_pLeft = NULL;
    pNode->m_pRight = NULL;
    pNode->m_pParent = NULL;
    
    return pNode;
}

// 链接父子节点元素
void ConnectTreeNodes(BinaryTreeNode* pParent, BinaryTreeNode* pLeft, BinaryTreeNode* pRight) {
    pParent->m_pLeft = pLeft;
    pParent->m_pRight = pRight;
    if (pLeft != NULL) pLeft->m_pParent = pParent;
    if (pRight != NULL) pRight->m_pParent = pParent;
}

BinaryTreeNode* GetNext(BinaryTreeNode* pNode) {
    
    if (pNode == NULL) return NULL;

    BinaryTreeNode* pNext = NULL;
    
    if (pNode->m_pRight != NULL) {
        BinaryTreeNode* pCurrent = pNode->m_pRight;
        while (pCurrent->m_pLeft != NULL) {
            pCurrent = pCurrent->m_pLeft;
        }
        pNext = pCurrent;
    } else if (pNode->m_pParent != NULL) {
        BinaryTreeNode* pCurrent = pNode;
        while (pCurrent->m_pParent != NULL && pCurrent == pCurrent->m_pParent->m_pRight) {
            pCurrent = pCurrent->m_pParent;
        }
        pNext = pCurrent->m_pParent;
    }
    return pNext;
}

int main(int argc, const char * argv[]) {
    
    BinaryTreeNode* pNodeA = CreateBinaryTreeNode('a');
    BinaryTreeNode* pNodeB = CreateBinaryTreeNode('b');
    BinaryTreeNode* pNodeC = CreateBinaryTreeNode('c');
    BinaryTreeNode* pNodeD = CreateBinaryTreeNode('d');
    BinaryTreeNode* pNodeE = CreateBinaryTreeNode('e');
    BinaryTreeNode* pNodeF = CreateBinaryTreeNode('f');
    BinaryTreeNode* pNodeG = CreateBinaryTreeNode('g');
    BinaryTreeNode* pNodeH = CreateBinaryTreeNode('h');
    BinaryTreeNode* pNodeI = CreateBinaryTreeNode('i');
    
    ConnectTreeNodes(pNodeA, pNodeB, pNodeC);
    ConnectTreeNodes(pNodeB, pNodeD, pNodeE);
    ConnectTreeNodes(pNodeC, pNodeF, pNodeG);
    ConnectTreeNodes(pNodeE, pNodeH, pNodeI);
    
    BinaryTreeNode* pNode = GetNext(pNodeA);
    
    if (pNode == NULL) {
        printf("当前为最后一个节点，或者输入无效\n");
    } else {
        printf("当前节点的下一个节点为 %c\n", pNode->m_nValue);
    }
    
    return 0;
}

5. 数据结构 - 栈和队列

栈是一个非常常见的数据结构，比如操作系统会给每个线程创建一个栈用来存储函数调用时各个函数的参数、返回地址和临时变量等。栈的特点是后进先出，即最后被 Push 栈的元素会第一个被 Pop。通常栈是一个不考虑排序的数据结构，我们需要 O(n) 时间才能找到栈中最大或者最小的元素，如果想要在 O(1) 时间内得到栈的最大值或者最小值，则需要对栈做特殊的设计。

队列是另外一种很重要的数据结构，和栈不同的是，队列的特点是先进先出。

面试题 9

题目：用两个栈实现队列。请实现队列中的两个函数 appendTail 和 deleteHead，分别完成在队列尾部插入节点和在队列头部删除节点的功能。

这道题的意图是要求我们操作这两个「先进后出」的栈实现一个「先进先出」的队列。我们通过一个具体的例子来分析往该队列插入和删除元素的过程。首先插入一个元素 a，先把它插入 stack1，此时 stack1 中有元素 { a }，stack2 为空。再压入两个元素 b 和 c，还是插入 stack1，此时 stack1 中的元素有 { a, b, c }，其中 c 位于栈顶，而 stack2 仍然为空。

这时候我们从队列中删除一个元素，按照队列先入先出的规则，由于 a 比 b、c 先插入队列中，最先被删除的元素应该是 a。元素 a 存储在 stack1 中，但并不在栈顶上，因此不能直接删除。所以我们把 stack1 中的元素逐个弹出并压入 stack2，stack1 为空，而 stack2 中的元素是 { c, b, a }，这时候就可以弹出 stack2 的栈顶 a 了。

从上面的分析中我们可以总结出：当 stack2 不为空时，在 stack2 中的栈顶元素是最先进入队列的元素，可以弹出。当 stack2 为空时，我们把 stack1 中的元素逐个弹出并压入 stack2。由于先进入队列的元素被压到 stack1 的底端，经过弹出和压入操作之后就处于 stack2 的顶端，又可以直接弹出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
char stack1[100] = {};
char stack2[100] = {};

// 在队列末尾添加一个结点
void appendTail(char c) {
    for (int i = 0; i < sizeof(stack1) / sizeof(char); i++) {
        if (stack1[i] == '\0') {
            stack1[i] = c;
            break;
        }
    }
}

// 在队列头部删除一个结点
void deleteHead() {
    if (stack2[0] == '\0') {
        for (int i = 0; i < sizeof(stack1) / sizeof(char); i++) {
            if (stack1[i] == '\0') {
                for (int j = 0; j < i; j++) {
                    stack2[j] = stack1[i - j - 1];
                    stack1[i - j - 1] = '\0';
                }
                break;
            }
        }
    }
    for (int i = sizeof(stack2) / sizeof(char) - 1; i >= 0; i--) {
        if (stack2[i] != '\0') {
            stack2[i] = '\0';
            break;
        }
    }
}

void printQueue() {
    for (int i = sizeof(stack2) / sizeof(char) - 1; i >= 0; i--) {
        if (stack2[i] != '\0') {
            printf("%c\t", stack2[i]);
        }
    }
    for (int i = 0; i < sizeof(stack1) / sizeof(char); i++) {
        if (stack1[i] != '\0') {
            printf("%c\t", stack1[i]);
        }
    }
    printf("\n");
}

int main(int argc, const char * argv[]) {
    
    appendTail('a');
    appendTail('b');
    appendTail('c');
    printQueue();
    
    deleteHead();
    printQueue();
    
    appendTail('d');
    printQueue();
    
    return 0;
}

面试题 9 - 附

题目：用两个队列实现一个栈。

我们通过一系列栈的压入和弹出操作来分析用两个队列模拟一个栈的过程。我们先往栈内压入一个元素 a，由于两个队列现在都是空的，我们可以选择把 a 插入两个队列的任意一个，不妨把 a 插入 queue1。接下来继续往 queue1 压入 b、c 两个元素，这个时候 queue1 包含了 3 个元素 { a, b, c }。

现在我们从栈内弹出一个元素，根据栈的后入先出原则，最后被压入栈的 c 应该最先被弹出。由于 c 位于 queue1 的尾部，而我们每次只能从队列的头部删除元素，因此我们可以先从 queue1 中依次删除元素 a、b 并插入 queue2，再从 queue1 中删除元素 c，这就相当于从栈中弹出元素 c 了。我们可以用同样的方法从栈内弹出元素 b。

接下来我们考虑往栈内压入一个元素 d，此时 queue1 已经有一个元素，我们就把 d 插入 queue1 的尾部。如果我们再从栈内弹出一个元素，那么此时被弹出的应该是最后被压入的 d。由于 d 位于 queue1 的尾部，我们只能先从头删除 queue1 的元素并插入 queue2，直到在 queue1 中遇到 d 再直接把它删除。

6. 算法和数据操作 - 递归和循环

递归是在一个函数的内部调用这个函数自身，而循环则是通过设置计算的初始值和终止条件，在一个范围内重复运算。通常递归的代码会比较简洁，在树的前序、中序、后序遍历算法的代码中，递归的实现明显要比循环简单得多。在面试的时候，如果面试官没有特别的要求，可以尽量多采用递归的方法编程。递归虽然有简洁的优点，但它同时也有显著的缺点：

  1. 递归由于是函数调用自身，而函数调用是有时间和空间的消耗的：每一次函数调用，都需要在内存栈中分配空间以保存参数、返回地址和临时变量，而且往栈里压入数据和弹出数据都需要时间，所以递归实现的效率不如循环；
  2. 递归中有可能很多计算都是重复的，从而对性能带来很大的负面影响。递归的本质是把一个问题分解成两个或者多个小问题。如果多个小问题存在相互重叠的部分，就存在重复的计算；
  3. 除效率之外，递归还有可能引起更严重的问题：调用栈溢出。在前面的分析中提到需要为每一次函数调用在内存栈中分配空间，而每个进程的栈的容量是有限的，当递归调用的层级太多时，就会超出栈的容量，从而导致调用栈溢出。

面试题 10 - 1

题目：斐波那契数列。写一个函数，输入 n，求斐波那契数列的第 n 项。斐波那契数列的定义如下：

IMG003

方法一，很多 C 语言教科书在讲述斐波那契数列的时候，常用递归的解法，效率很低，挑剔的面试官不会喜欢。我们以求解 f(10) 为例来分析递归的求解过程，用树形结构来表示这种依赖关系，如下图所示：

IMG004

我们不难发现，在这棵树中有很多节点是重复的，而且重复的节点数会随着 n 的增大而急剧增加，用递归方法计算的时间复杂度是以 n 的指数的方式递增的。读者不妨求斐波那契数列的第 100 项试试，感受一下这样递归会慢到什么程度。

1
2
3
4
5
6
7
8
9
10
11
12
long long Fibonacci(unsigned int n) {
    if (n <= 0) return 0;
    if (n == 1) return 1;
    return Fibonacci(n - 1) + Fibonacci(n - 2);
}

int main(int argc, const char * argv[]) {
    
    printf("%lld\n", Fibonacci(10));
    
    return 0;
}

方法二，上述递归代码之所以慢，是因为重复的计算太多。我们可以从下往上计算，首先根据 f(0) 和 f(1) 算出 f(2)，在根据 f(1) 和 f(2) 算出 f(3)，以此类推就可以算出第 n 项了，这种思路的时间复杂度是 O(n) 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
long long Fibonacci(unsigned int n) {
    
    if (n <= 0) return 0;
    if (n == 1) return 1;
    
    long long fibNMinusOne = 1;
    long long fibNMinusTwo = 0;
    long long fibN = 0;
    for (unsigned int i = 2; i <= n; i++) {
        fibN = fibNMinusOne + fibNMinusTwo;
        fibNMinusTwo = fibNMinusOne;
        fibNMinusOne = fibN;
    }
    return fibN;
}

int main(int argc, const char * argv[]) {
    
    printf("%lld\n", Fibonacci(100));
    
    return 0;
}

方法三

IMG005

代码地址：https://github.com/zhedahht/CodingInterviewChinese2/blob/master/10_Fibonacci/Fibonacci.cpp

面试题 10 - 2

题目：青蛙跳台阶问题。一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级台阶。求该青蛙跳上一个 n 级台阶总共有多少种跳法。

首先我们考虑最简单的情况：只有 1 级台阶，那显然只有一种跳法；如果有 2 级台阶，可以跳两次，一次跳 1 级，或者跳一次，跳 2 级。

接着我们再来讨论一般情况：我们把 n 级台阶时的跳法看成 n 的函数 f(n)，当 n > 2 时，第一次跳的时候就有两种不同的选择：一是第一次只跳 1 级，此时跳法数目等于后面剩下的 n - 1 级台阶的跳法数目，即为 f(n-1)；二是第一次跳 2 级，此时跳法数目等于后面剩下的 n - 2 级台阶的跳法数目，即为 f(n-2)。因此，n 级台阶的不同跳法的总数 f(n)=f(n-1)+f(n-2)。分析到这里，我们不难看出这实际上就是斐波那契数列了。

面试题 10 - 附 1

题目：在青蛙跳台阶的问题中，如果把条件改成：一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级台阶，也可以跳上 n 级台阶，此时该青蛙跳上一个 n 级的台阶总共有多少种跳法？

我们用数学归纳法可以证明 f(n)=2^(n-1)。

面试题 10 - 附 2

题目：我们可以用 2×1 的小矩形横着或者竖着去覆盖更大的矩形。请问用 8 个 2×1 的小矩形无重叠地覆盖一个 2×8 的大矩形，总共有多少种方法？

IMG006

同样是斐波那契数列。

7. 算法和数据操作 - 查找和排序

查找和排序都是在程序设计中经常用到的算法。查找相对而言较为简单，不外乎顺序查找、二分查找、哈希表查找和二叉排序树查找。在面试的时候，不管是用循环还是用递归，面试官都期待应聘者能够信手拈来写出完整正确的二分查找代码。哈希表和二叉排序树查找的重点在于考察对应的数据结构而不是算法。哈希表最主要的优点是我们利用它能够在 O(1) 时间内查找某一元素，但其缺点是需要额外的空间来实现哈希表。

排序比查找要复杂一些，面试官会经常要求应聘者比较插入排序、冒泡排序、归并排序、快速排序等不同算法的优劣。强烈建议应聘者对各种排序算法的特点烂熟于胸，能够从额外空间消耗、平均时间复杂度和最差时间复杂度等方面去比较它们的优缺点。很多公司的面试官喜欢在面试环节要求应聘者写出快速排序的代码。

实现快速排序算法的关键在于先在数组中选择一个数字，接下来把数组中的数字分为两部分，比选择的数字小的数字移到数组的左边，比选择的数字大的数字移到数组的右边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
void Swap(int* x, int* y) {
    int t = *x;
    *x = *y;
    *y = t;
}

// 分区
int Partition(int arr[], int start, int end) {

    // 小于参考值的最后一个数的角标
    int lastSmall = start - 1;
    
    for (int i = start; i < end; i++) {
        // 将 arr[end] 作为参考值
        if (arr[i] < arr[end]) {
            lastSmall++;
            if (lastSmall != i) {
                Swap(&arr[i], &arr[lastSmall]);
            }
        }
    }
    
    // 最后将参考值和大于或等于参考值第一个数交换
    Swap(&arr[lastSmall + 1], &arr[end]);
    
    return lastSmall + 1;
}

void QuickSort(int arr[], int start, int end) {
    
    if (start == end) return;
    
    int index = Partition(arr, start, end);
    
    if (index > start) {
        QuickSort(arr, start, index - 1);
    }
    if (index < end) {
        QuickSort(arr, index + 1, end);
    }
}

int main(int argc, const char * argv[]) {
    
    int arr[] = { 4, 1, 2, 5, 3, 4, 7 };
    
    QuickSort(arr, 0, sizeof(arr) / sizeof(int) - 1);
    
    for (int i = 0; i < sizeof(arr) / sizeof(int); i++) {
        printf("%d\t", arr[i]);
    }
    
    return 0;
}

不同的排序算法适用的场合也不尽相同，快速排序虽然总体的平均效率是最好的，但也不是任何时候都是最优的算法。在面试的时候，如果面试官要求实现一个排序算法，那么应聘者一定要问清楚这个排序应用的环境是什么、有哪些约束条件、是否可以用辅助内存。比如对公司员工年龄进行排序，下面的方法用长度 100 的整数数组作为辅助控件换来了 O(n) 的时间效率：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void SortAges(int ages[], int length) {
    
    if (ages == NULL || length <= 0) return;
    
    // 公司员工年龄范围 0 ~ 99
    const int oldestAge = 99;
    
    // 统计每个年龄出现的次数
    int timesOfAge[oldestAge + 1];
    for (int i = 0; i <= oldestAge; i++) {
        timesOfAge[i] = 0;
    }
    
    for (int i = 0; i < length; i++) {
        timesOfAge[ages[i]]++;
    }
    
    int index = 0;
    for (int i = 0; i <= oldestAge; i++) {
        for (int j = 0; j < timesOfAge[i]; j++) {
            ages[index] = i;
            index++;
        }
    }
}

面试题 11

题目：旋转数组的最小数字。把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如，数组 { 3, 4, 5, 1, 2 } 为 { 1, 2, 3, 4, 5 } 的一个旋转，该数组的最小值为 1。

本题给出的数组在一定程度上是排序的，因此我们可以用二分查找法的思路来寻找这个最小的元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
int MinInOrder(int* numbers, int index1, int index2) {
    
    int result = numbers[index1];
    for (int i = index1 + 1; i <= index2 ; i++) {
        if (result > numbers[i]) {
            result = numbers[i];
        }
    }
    return result;
}

int Min(int* numbers, int length) {
    
    int index1 = 0;
    int index2 = length - 1;
    int indexMid = index1;
    
    while (numbers[index1] >= numbers[index2]) {
        
        // 如果 index1 和 index2 指向相邻的两个数，则 index1 指向第一个递增子数组的最后一个数字，index2 指向第二个子数组的第一个数字，也就是数组中的最小数字
        if (index2 - index1 == 1) {
            indexMid = index2;
            break;
        }
        
        indexMid = (index1 + index2) / 2;
        
        // 如果下标为 index1、index2 和 indexMid 指向的三个数字相等，则只能顺序查找
        if (numbers[index1] == numbers[index2] && numbers[index1] == numbers[indexMid]) {
            return MinInOrder(numbers, index1, index2);
        }
        
        // 缩小查找范围
        if (numbers[indexMid] >= numbers[index1]) {
            index1 = indexMid;
        } else if (numbers[indexMid] <= numbers[index2]) {
            index2 = indexMid;
        }
    }
    return numbers[indexMid];
}

int main(int argc, const char * argv[]) {
    
    int numbers[5] = { 3, 4, 5, 1, 2 };
    
    int min = Min(numbers, sizeof(numbers) / sizeof(int));
    
    printf("%d\n", min);
  
    return 0;
}

8. 算法和数据操作 - 回溯法

如果面试题要求在二维数组（可能具体表现为迷宫或者棋盘等）上搜索路径，那么我们可以尝试用回溯法。通常回溯法很适合用递归的代码实现。只有当面试官限定不可以用递归实现的时候，我们再考虑用栈来模拟递归的过程。

回溯法可以看成蛮力法的升级版，它从解决问题每一步的所有可能选项里系统地选择出一个可行的解决方案。回溯法非常适合由多个步骤组成的问题，并且每个步骤都有多个选项。当我们在某一步选择了其中一个选项时，就进入下一步，然后又面临新的选项。我们就这样重复选择，直至到达最终的状态。

用回溯法解决的问题的所有选项可以形象地用树状结构表示，树的叶节点对应着终结状态，如果在叶节点的状态满足题目的约束条件，那么我们找到了一个可行的解决方案。如果在叶节点的状态不满足约束条件，那么只好回溯到它的上一个节点再尝试其他的选项。

面试题 12

题目：矩阵中的路径。请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始，每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格，那么该路径不能再次进入该格子。例如，在下面的 3×4 的矩阵中包含一条字符串 bfce 的路径，但矩阵中不包含字符串 abfb 的路径，因为字符串的第一个字符 b 占据了矩阵中的第一行第二个格子之后，路径不能再次进入这个格子。

IMG007

这是一个可以用回溯法解决的典型题，由于回溯法的递归特性，路径可以被看成一个栈。当在矩阵中定位了路径中前 n 个字符的位置之后，在与第 n 个字符对应的格子的周围都没有找到第 n+1 个字符，这时候只好在路径上回到第 n-1个字符，重新定位第 n 个字符。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
bool hasPathCore(const char* matrix, int rows, int cols, int row, int col, const char* str, int pathLength, bool* visited) {
    
    if (str[pathLength] == '\0') return true;
    
    bool hasPath = false;
    if (row >= 0 && row < rows && col >= 0 && col < cols && matrix[row * cols + col] == str[pathLength] && visited[row * cols + col] == false) {
        
        pathLength++;
        visited[row * cols + col] = true;
        
        hasPath =
            hasPathCore(matrix, rows, cols, row, col - 1, str, pathLength, visited) ||
            hasPathCore(matrix, rows, cols, row - 1, col, str, pathLength, visited) ||
            hasPathCore(matrix, rows, cols, row, col + 1, str, pathLength, visited) ||
            hasPathCore(matrix, rows, cols, row + 1, col, str, pathLength, visited);
        
        if (!hasPath) {
            pathLength--;
            visited[row * cols + col] = false;
        }
    }
    return hasPath;
}

bool hasPath(const char* matrix, int rows, int cols, const char* str) {
    
    if (matrix == NULL || rows < 1 || cols < 1 || str == NULL) return false;
    
    int pathLength = 0;
    for (int row = 0; row < rows; row++) {
        for (int col = 0; col < cols; col++) {
            
            // 布尔值矩阵，用来标识路径是否已经进入了每个格子
            bool visited[rows * cols];
            if (hasPathCore(matrix, rows, cols, row, col, str, pathLength, visited)) {
                return true;
            }
        }
    }
    
    return false;
}

int main(int argc, const char * argv[]) {
    
    const char* matrix = "ABTGCFCSJDEH";
    const char* str = "BFCE";
    
    BOOL has = hasPath(matrix, 3, 4, str);
       
    printf("%d\n", has);
    
    return 0;
}

面试题 13

题目：机器人的运动范围。地上有一个 m 行 n 列的方格，一个机器人从坐标 (0, 0) 的格子开始移动，它每次可以向左、右、上、下移动一格，但不能进入行坐标和列坐标的数位之和大于 k 的格子。例如，当 k 为 18 时，机器人能够进入方格 (35, 37)，因为 3+5+3+7=18。但它不能进入方格 (35, 38)，因为 3+5+3+8=19。请问该机器人能够到达多少个格子？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
int getDigitSum(int number) {
    return number / 1 % 10 + number / 10 % 10;
}

int movingCountCore(int threshold, int rows, int cols, int row, int col, bool* visited) {
    
    int count = 0;
    
    if (row >= 0 && row < rows && col >= 0 && col < cols && getDigitSum(row) + getDigitSum(col) <= threshold && visited[row* cols + col] == false) {
        
        visited[row * cols + col] = true;
        
        count += 1;
        count += movingCountCore(threshold, rows, cols, row - 1, col, visited);
        count += movingCountCore(threshold, rows, cols, row, col - 1, visited);
        count += movingCountCore(threshold, rows, cols, row + 1, col, visited);
        count += movingCountCore(threshold, rows, cols, row, col + 1, visited);
    }
    return count;
}

int movingCount(int threshold, int rows, int cols) {
    
    if (threshold < 0 || rows <= 0 || cols <= 0) return 0;
    
    bool visited[rows * cols];
    for (int i = 0; i < rows * cols; i++) {
        visited[i] = false;
    }
    
    int count = movingCountCore(threshold, rows, cols, 0, 0, visited);
    
    return count;
}

int main(int argc, const char * argv[]) {
    
    int rows = 10;
    int cols = 10;
    int threshold = 5;
    
    int count = movingCount(threshold, rows, cols);
       
    printf("%d\n", count);
    
    return 0;
}

9. 算法和数据操作 - 动态规划与贪婪算法

如果面试题是求某个问题的最优解，并且该问题可以分为多个子问题，那么我们可以尝试用动态规划。在用自上而下的递归思路去分析动态规划问题的时候，我们会发现子问题之间存在重叠的更小的子问题。为了避免不必要的重复计算，我们用自下而上的循环代码来实现，也就是把子问题的最优解先算出来并用数组（一维或者二维数组）保存下来，接下来基于子问题的解计算大问题的解。

如果我们告诉面试官动态规划的思路之后，面试官还在提醒说再分解子问题的时候是不是存在某个特殊的选择，如果采用这个特殊的选择将一定能得到最优解，那么，通常面试官这样的提示意味着该面试题可能适用于贪婪算法。当然面试官也会要求应聘者证明贪婪选择的确最终能够得到最优解。

面试题 14

题目：剪绳子。给你一根长度为 n 的绳子，请把绳子剪成 m 段（m、n 都是整数，n>1，m>1），每段绳子的长度记为 k[0], k[1], ···, k[m]。请问 k[0] × k[1] × ··· × k[m] 可能的最大乘积是多少？例如，当绳子的长度是 8 时，我们把它剪成长度分别为 2、3、3 的三段，此时得到的最大乘积是 18。

方法一，动态规划。

10. 算法和数据操作 - 位运算

位运算可以看成一类特殊的算法，它是把数字表示成二进制之后对 0 和 1 的操作。一般总共只有与、或、异或、左移和右移 5 种位运算。